Note-Taking Strategies

NOTE-TAKING STRATEGIES OVERVIEW
​My students are no more than two years away from attending college, so it is a priority for them to develop excellent note-taking strategies. My goal is for students to develop skills such as annotating text, rewording vocabulary, summarizing verbal and written key points, and organizing mathematical thinking. I expose my students to notes that follow a PowerPoint presentation format, because the format is highly used in university settings. I model note-taking and use positive narration, circulation, and scaffolded questions to engage students.

After exploring key terms and concepts, I use a gradual release model to engage my students in example problems. My students first actively observe and participate in an example that I model solving on the board. Then, students work as a whole class to solve a similar, but less scaffolded problem, which I call a "You Try". The You Try is led by several students who solve the problem on the board. Next, students work independently for 8 minutes on the classwork, in order to self-assess how much they know. Finally, students work with their desk partners for 10 minutes to complete the classwork. During this time, I am also circulating the classroom to help students in small groups and individually.

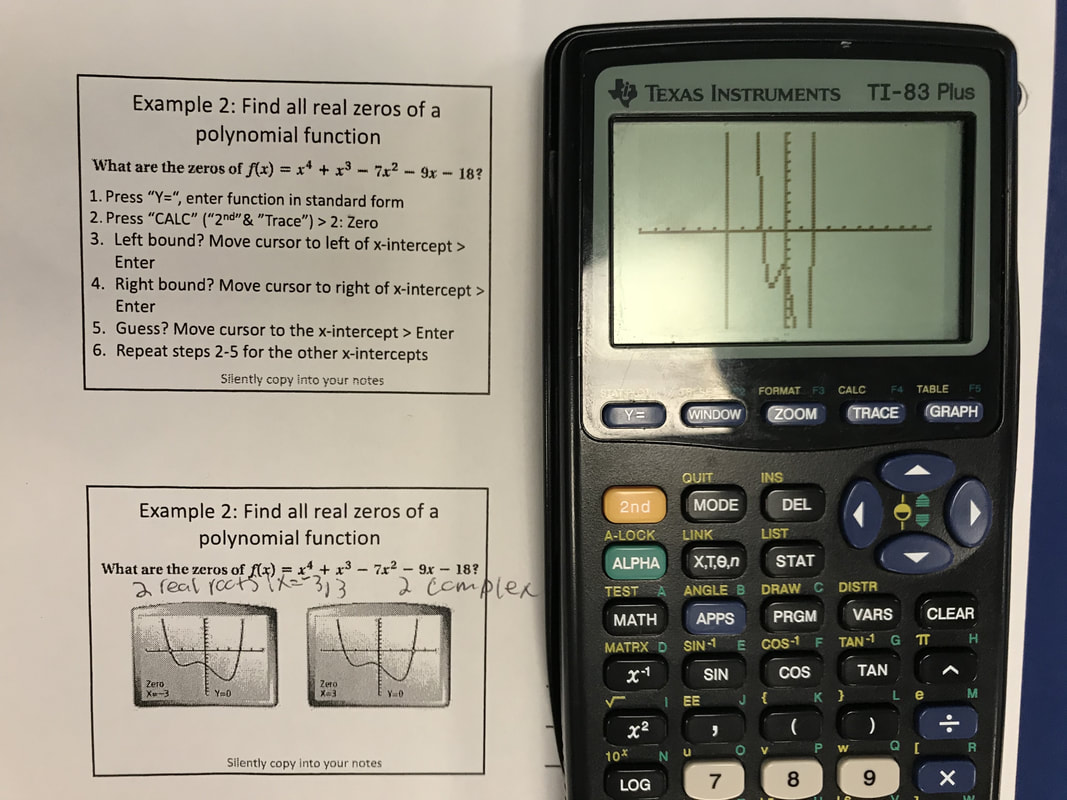
There are a tremendous number of intersections between mathematics and technology, so I integrate technology into every lesson in my Algebra II curriculum. We frequently use videos, online activities, games, and surveys to enhance instruction and practice real-world applications. In addition, graphing calculators are a primary method of technology integration in my classroom. At the beginning of the school year, I communicate to parents and guardians via a paper newsletter that their child is required to bring a graphing calculator to class each day. I explicitly teach students how to use their graphing calculators by engaging them in calculator exploration activities and showing them specific calculator techniques through a document camera.

Please scroll down or click on the table of contents below to learn more about my guided notes, gradual release model, and integrated technology.

TABLE OF CONTENTS
Guided Notes
Gradual Release Model
Integrated Technology

Guided Notes
Each day as my students enter the classroom, they receive handout with key slides from the lesson presentation. ​I create the lesson presentation using resources such as Pearson's Algebra II Common Core, Teaching Tolerance, Better Lesson, and Eureka Math. Each day, students first write the daily objective at the top of their handout. Then, we discuss the key terms. Student volunteers read each key term and offer ideas on how to annotate, summarize, and reword the key terms. Through discussion, students come to an agreement on note-taking strategies, and I offer final feedback. In addition, I probe for learner understanding by asking questions about the key terms. While students generally mirror their handout to the annotations, summaries, and rewording agreed upon by the whole class, I highly encourage students to take notes in a way that is most useful to their diverse learning needs.

The images below present the key terms on the objective that students will be able to use the Fundamental Theorem of Algebra to determine the total number of roots, and graphically determine the number of real versus complex roots. Students drew a connection between "degree" and "highest exponent", and also drew connections between "roots", "x-intercepts" and "zeros". Students defined real solutions as solutions that can be seen, and complex solutions as solutions with imaginary numbers. Students analyzed the three graphs and determined the number of real and complex roots for each graph. Finally, students concluded that the total number of roots equals the sum of real and complex roots. The variations in students' notes below depict how I encourage students to take notes that are personally relevant.

Gradual Release Model
In a gradual release model, I guide my students towards independent complex thinking, meaningful tasks, and peer collaboration. The lesson structure transitions from teacher-centered, to whole class-centered, to partner and individual practice. In addition, the variety of instructional strategies used in a gradual release model strengthens my students' communication skills through speaking, listening, reading, and writing. First, I demonstrate how to solve an example problem by framing the example in its objective, giving direct instruction, thinking out loud, and modeling an exemplar. In addition, I ask scaffolded questions that use students' prior learning to help them draw connections to the new material.

Second, students interactively practice new concepts through You Trys. During You Trys, I provide prompts, clues, and checks to guide learning. Several student volunteers come to the front board to write out their mathematical thinking, and other students explain and provide feedback. The whole class is involved in You Trys, as we use hand signals and white boards to instantly gauge comprehension. If comprehension is low, I explain the example again using different language and visuals.

Finally, students take on full responsibility for the learning objective by working independently on classwork. They work silently and individually for 8 minutes, using only their notes for assistance. Then, students work with their desk partners for 10 minutes to support each other by asking questions and challenging answers. My co-teacher and I circulate the classroom to provide additional supports to students based on their mastery level.

In the images below, students are finding the real roots of polynomial equations. The example provides step-by-step, written scaffolding, the You Try uses verbal clues, and the lesson worksheet has no scaffolding. Just as I encourage students to take notes that are personally relevant, students continue to customize their notes in the examples, You Trys, and classwork. As seen below, students correctly show the process to finding real roots; however, some students include additional notes that they independently determined were relevant for their learning.

Integrated Technology
Graphing calculator mastery is core to my Algebra II instruction. Most of the Algebra II curriculum focuses on various function families, and graphing calculators provide an excellent way to visualize and solve functions. Students generally first solve problems without graphing calculators, in order to develop strong conceptual understanding. However, I also embed graphing calculator learning into each lesson, for graphing calculator mastery is a real-world skill. 

In the images below, students have already learned how to find real roots by factoring in example 1. In example 2, students learn how to find real roots by using the zero function in their graphing calculators.  I have found that my diverse learners have different preferences for finding real roots. Therefore, I engage students in multiple models of solving for real roots: factoring and graphing. The calculator steps are on each students' handout, and I model the steps on the front board using a document camera and graphing calculator. I apply a gradual release model to all lesson examples, so the responsibility for the learning outcome will shift to the student through the You Try and classwork. 
Picture
Student has just completed step 1 and graphed the function. Student did not perform step 2, so the calculator will not find the zeros. I used this students' mistake as a learning opportunity, and asked the student how he could visualize the zeros without using the zero function.
Picture
Student has just completed step 2. Student asked how to move the cursor to the left of the x-intercepts, as the cursor is currently out of view. This student's question prompted a discussion about the limited window view of the graphing calculator and how it could be adjusted.