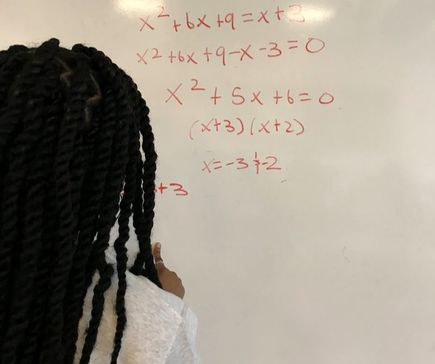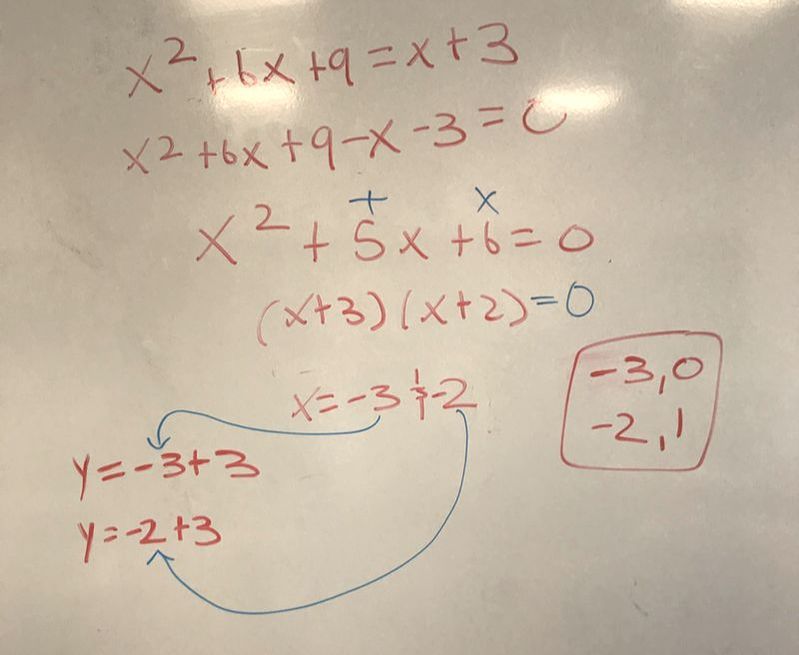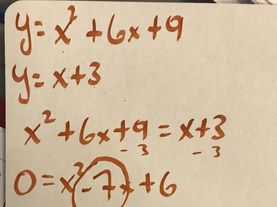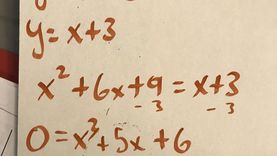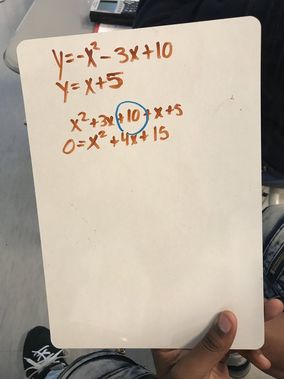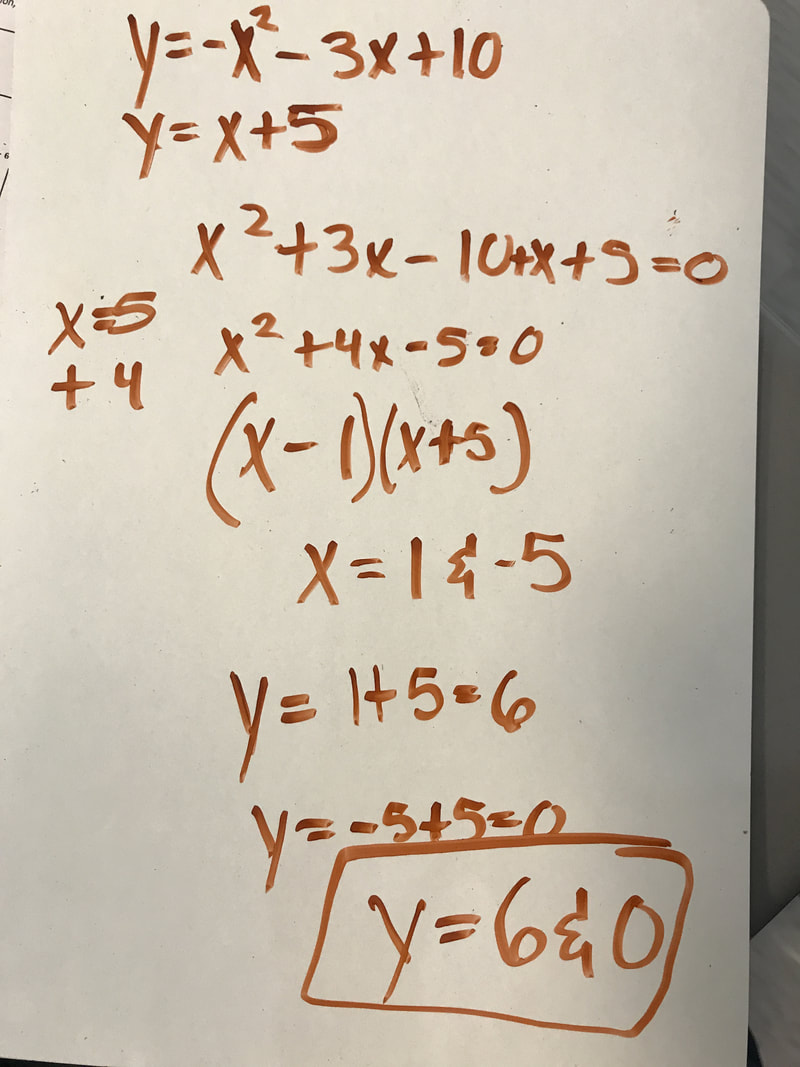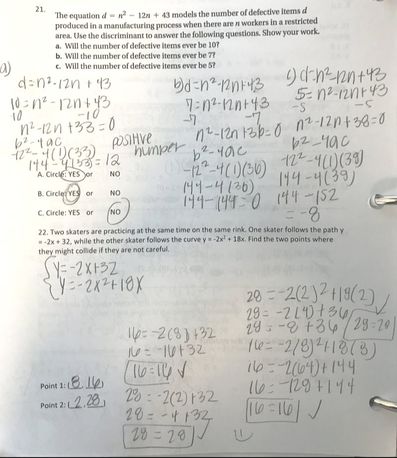Algebra II Mastery

ALGEBRA II OVERVIEW
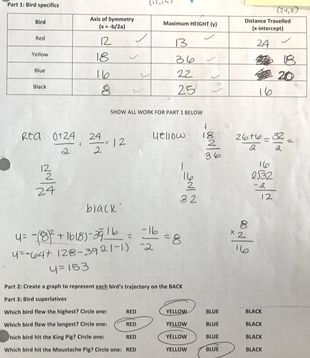
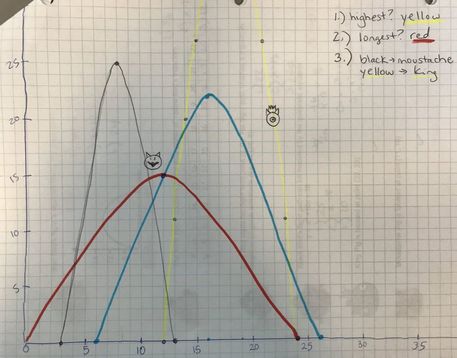
Algebra II is a continuation of algebraic and geometric concepts developed in Algebra I and Geometry. For most of my students Algebra II is their final full-year high school mathematics course. Students review solving linear expressions, equations, and inequalities. Then, they learn how to express functions and solve equations in function families such as quadratic, polynomial, radical, rational, logarithmic, and periodic functions. Arithmetic and geometric sequences and series, and probability and statistics are also explored.

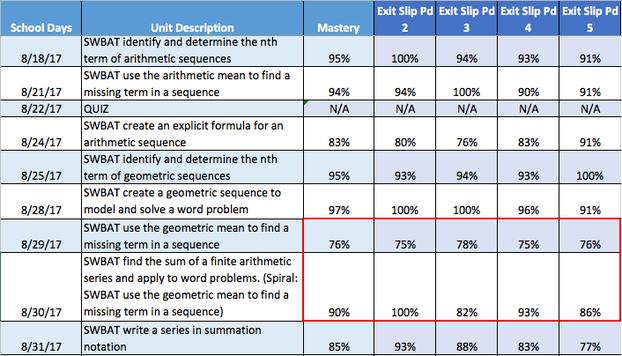
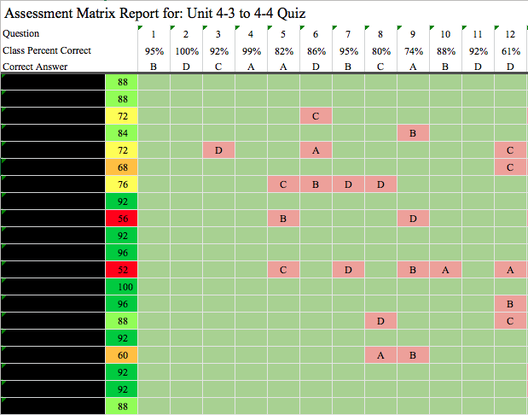
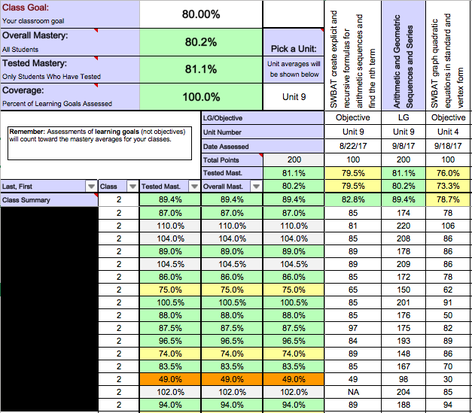
My curriculum is comprised of units. Each function family or topic is a single unit. During a unit, student mastery is assessed daily through formative assessments, and weekly through summative assessments. Formative assessments allow me to quickly determine the depth of student understanding and address common mistakes. Summative assessments such as major quizzes, tests, and projects gauge long-term understanding and application of Algebra II standards. My students and I regularly track progress on formative and summative assessments.

Please scroll down or click the table of contents below to learn more about my formative assessments, summative assessments, special education accommodations, and data-driven instruction in Algebra II.

TABLE OF CONTENTS
Formative Assessments in Algebra II
Summative Assessments in Algebra II
Special Education Accommodations
Data-Driven Instruction in Algebra II

Formative Assessments in Algebra II

In every lesson, my students are assessed through homework completion checks, white board "You Trys", classwork check-ins, and exit tickets. Even more informally, hand signals are used throughout the lesson to gauge the level of understanding. Formative assessments range from whole-class to individual check-ins, and from teacher-graded to student-graded items. Whole-class assessments such as hand signals and white board You Trys help me to instantly adjust the pacing of the lesson. I use individual check-ins during classwork time to further scaffold material and re-teach students. Teacher-graded items such as exit tickets depict student mastery of the daily objective. Student-graded items such as homework completion checks, give students the chance to independently determine and fix their errors.

WHITE BOARD YOU TRYS
After I do an example on the board showing how to master our Algebra II daily objective, students use their mini white boards to complete a You Try problem. You Try problems are aligned to the daily objective and scaffolded similarly to the example problem just shown. As students work independently on the You Try, I circulate the classroom to note any common errors. After the timer, all students raise their white boards, and one student with the correct process comes up to the white board at the front of the classroom to show their work. Then, another classmate also with the correct process will explain the first classmate's steps. Next, all students will circle any errors on their mini white board, and correct their answers. Finally, all students will raise their mini white boards with corrected steps.

A student is writing the correct process for solving a linear-quadratic system on the front board.

Another student explained and annotated the first student's work with additional clarifying comments.

CLASSWORK CHECK-INS
During the middle of the class period, assessments shifts from whole-class to individualized assessments. I use classwork check-ins to provide individual feedback and help to my students. Students independently complete the classwork and can choose to work directly on the guided classwork packet, or on a mini white board. Students may use their notes and partner pairs for resources. While students are working, I am circulating the classroom to spot check classwork and note common errors. If there is a common error on at least 3 packets or mini white boards, I bring the class back to center to making clarifying comments. This real-time analysis of assessment data allows me to quickly understand patterns and gaps in learning, to adjust my instruction and to provide meaningful feedback to all learning.

A student made the error of subtracting both 6x and x from both sides, and circled his error.

Continuing from the picture above: the student fixed his error to subtract only x from both sides of the equation.

A student circled his error of not changing the sign on 10.

Continuing from the center picture: the student fixed his error and correctly found the y-values of the system.

HOMEWORK COMPLETION CHECKS
Another daily summative assessment is the homework completion check. Homework answers are posted on the board, so students can self-check and correct their homework. I circulate the classroom to check homework for completion by marking a homework tracker. At the end of the week, I collect the homework trackers and grade homework for thorough completion.

Students then track their accuracy by writing their score on the homework sheet and saving it in the homework section of their binders. Then, we review any homework problems that students were not able to resolve independently. There are usually 1-3 questions we review as a whole class.

This is a student's corrected homework on the zero product property. He had struggled with knowing when a solution was positive or negative, but self-assessed and fixed his error.

EXIT TICKETS
During the last 5 minutes of class, students complete an exit ticket. The exit ticket is a single multiple-choice question that is aligned to our daily objective. Students work silently and independently on the exit ticket, and show their work to earn full credit. The exit ticket is not graded for accuracy, but determines if the objective needs to be re-taught and re-assessed the next day. If mastery is between 70-80% the objective is spiraled into the next day's lesson. If mastery is below 70%, the lesson is re-taught and re-assessed.

To the left are images of exit tickets from a lesson solving linear-quadratic systems through substitution. On this day, 100% of period 2 mastered the daily objective. Therefore, I continued onto the next objective in the following class, which was graphing linear-quadratic systems.

To the Top

Summative Assessments in Algebra II

Summative assessments are used to evaluate student mastery of Algebra II objectives after cycles of planning, implementation, formative assessment, and evaluation. Before a summative assessment, students have practiced numerous problems, engaged in formative assessments, and reviewed the objectives. Students have a major quiz, test, or project at the end of each week. The difference in naming conventions is due to the assessment style.

Since the ACT exam's mathematics section is all multiple-choice, in an effort to prepare all learners for the demands of the ACT, my quizzes are all multiple-choice with ACT-styled answer choices. On the other hand, tests are all short-answer, and often require students to engage in a multi-part word problem. Projects involve more tactile learning and creativity. Past projects have included designing a statistical experiment about a social cause, creating a music video featuring the quadratic formula, and creating a function family based on characteristics of extended family members.

Students are well-aware of assessment naming conventions, and the assessment schedule is clearly communicated, as all summative assessment dates and types are listed on the front and back board one month in advance. Altogether, summative assessments assess the breadth and depth of long-term retention and synthesis of specific unit objectives.

UNIT PROJECTS
Through unit projects, students can creatively demonstrate their mastery of many objectives within a unit. Projects also provide leadership opportunities for students, as students work on planning, collaboration, delegation, and presentation skills. There are at least two projects within each unit. In the quadratic function unit, students produced their own music video featuring the quadratic formula and how to use the discriminant. In another project, students mapped out the flight path of various Angry Birds. My projects are meant to be fun opportunities for students to demonstrate interdisciplinary, technology-based, and culturally relevant learning.

In the images to the right and below, students were given incomplete information about each Angry Bird. Students had to use multiple quadratic function skills such as graphing using points, using a table, and using the quadratic formula, in order to determine the path of each Angry Bird.

This student struggled with finding the distance travelled for the yellow and blue bird, as she did not realize that distance was "2x", not "x".

This student correctly graphed the path of each Angry Bird and named the Angry Bird superlatives.

UNIT QUIZZES
Unit quizzes consist of multiple-choice questions that are aligned to the Algebra II standards in the College and Career Readiness Standards (CCRS) set by the ACT exam. Questions are phrased similarly to those on the math section of the ACT exam. On almost every quiz, students encounter problems that involve defining math terms, solving equations, graphing, using a table, analyzing a graph, analyzing errors, and real-world application word problems.

Below are images from a unit quiz. On this page of the quiz, the following objectives were assessed:
1. Determine the quadratic function given 3 points, using the Quadratic Regression function on a graphing calculator
2. Use a table and the Quadratic Regression function on a graphing calculator to determine the quadratic function
3. Find the vertex by using the equation for axis of symmetry to find "x", and then solving for "y"
4. Solve real-world application problems about finding the minimum, maximum, or a given value in a quadratic function

This student used a mix of the substitution method and the Quadratic Regression application on her graphing calculator to correctly solve #1-6. Because she did not show work on problem #7 and chose an incorrect answer, she earned no credit.

This student predominantly used substitution method, but also some Quadratic Regression to correctly solve #1-7.

UNIT TESTS
Unit tests showcase the breadth and depth of student understanding and critical thinking. Unit tests cover 8 to 20 daily objectives. Unit tests consist of all real-world application problems. On almost every test, students engage in multiple-part word problems in which they need to solve equations, explain their reasoning, draw a diagram, create a table, plot a graph, use applications on a graphing calculator, define mathematical terms, and write instructional steps for someone learning the objective for the first time. As I align each test question to one of the daily objectives in the unit, test results inform me about mastery on specific objectives.

Below are images from the unit test on quadratic functions. In problem #21, the student on the left forgot to square the "b" value when finding discriminant. In addition, she only showed partial work, so it unclear how she arrived at her answer. I will work with her in a small group to review how to use the discriminant to determine the number of solutions. The student on the right solved problem #22, and correctly justified each part of the using using the sign of the discriminant. In problem #22, the student on the left used her graphing calculator to find the intersection of the linear and quadratic functions. The student on the right solved the system using substitution method. Both methods were acceptable, and both students showed mastery of solving linear-quadratic systems. By not requiring a specific method of solution, these two test show I was able to engage learners in multiple ways of demonstrating knowledge and skill as part of the assessment process.

To the Top

Special Education Accommodations

Since I teach one inclusion period with special education students, I create a special education version of all unit quizzes and tests. As all my students can and will learn in my classroom, I closely monitor special education, versus general education mastery. For each quiz and test, I calculate the special education and general education averages percentages. If the difference between the averages exceeds 5%, I collaborate with my special education co-teacher to have more pull-outs and scaffolded work on the objectives with the lowest mastery. Together, we track the individual learning goals of every student with an IEP, and inform their parents of progress twice a month through in-person meetings or phone calls.

Below on the left is an image of a modified quiz on quadratic functions, while the image on the right is the general education quiz. The special education version demands the same level of rigor as the general education version, but provides more scaffolding. For example, word problems are annotated on the special education version of exams. In addition, special education students can opt for small group testing, individual testing, and extended time.

This is a modified assessment. The x and y-coordinates are labelled for the student. In addition, the first step in factoring is hinted for #14-16.

This is a general education assessment.

To the Top

Data-Driven Instruction in Algebra II

Data-driven instruction is a critical to the success of my students because it informs me of the objectives they have mastered, partially mastered, and have not mastered. Mastery trackers house my assessment data. I use mastery trackers for both my formative and summative assessments.

After calculating the average class score on an assessment, I adjust my future lesson plans, so that my lessons build off the average level of understanding. I consider an average of 80% to be class mastery. If the class assessment average is above 80%, my students have mastered the assessed objectives, so I continue on to the next set of objectives. If the class assessment average is between 70% to 80%, I review objectives that were not mastered in future class lessons. If class mastery is below 70%, I re-teach the objectives using new strategies and then re-assess my students through an extended exit ticket.

Not only do I analyze class mastery, but I also differentiate learning by individual mastery. For my students who exceed the average mastery over 10%, I provide additional challenge problems that are still aligned to the daily objective, but require further critical thinking and application. For my students who are 10% or more below average mastery, I provide quiz and test correction sheets, additional scaffolding, small group interventions, and individual check-ins after school. Data-driven instruction increases student engagement and retention because my lessons are built off quantitative knowledge of whole-class and individual mastery.

FORMATIVE ASSESSMENTS: EXIT TICKET TRACKER AND RE-TEACH EVIDENCE
While I gather anecdotal data from circulating my classroom during formative assessments, it is also helpful to know exactly what percentage of students have mastered the daily objective before the following school day. During the last five minutes of class, my student complete an exit ticket which is aligned to our daily objective. The only exception is that students do not complete an exit ticket on days when we have a summative assessment such as a quiz or test. I collect and grade the exit ticket immediately after school. I use a exit ticket tracker to review mastery by class period and overall mastery.

Above, the image shows that mastery was below 80% on 8/29/17. Therefore, the same objective was taught again in the next day's lesson through several review problems on the classwork. The next day, 90% of my students mastered the spiraled and new objective, indicating that the re-teach was effective.

SUMMATIVE ASSESSMENTS: QUESTION-BY-QUESTION TRACKER
I use mastery trackers for unit quizzes and tests. I grade all quizzes and tests immediately after school, because I allot 10 minutes of the following class to re-teach and re-assess any objectives that show less than 70% mastery.
I use a question-by-question tracker that shows mastery for each question, and for each student.

To the right, is an image of the tracker used for a unit quiz on quadratic functions. For privacy, the student names have been omitted in the first column. While the overall class average for this quiz was above an 80%, a question-by-question tracker allows me to see if there are any particular objectives that still need to be reviewed. In this snapshot, students showed strong mastery of the objectives covered in questions #1-8, 10-11. However, student mastery was 74% for question #9, in which students had to first convert from function to coordinate point notation, and then use Quadratic Regression to find the quadratic function. This objective was spiraled into future lessons, through class notes.

In addition, mastery was a low 61% for question #12, which required students to do a careful reading, and apply critical thinking by solving for "y" first, and then "x" (which is reverse of the traditional order). I made note to re-teach and re-assess this objective the following day. The re-assessment question on the classwork showed mastery of 92%, so I knew that the re-teach was successful. In addition, I wrote down the names of all students who scored lower than a 70% on this quiz, and left them reminder notes in their mail boxes to come to my office hours after school for quiz corrections.

SUMMATIVE ASSESSMENTS: OVERVIEW TRACKER
For summative assessments, in addition to a question-by-question tracker, I also use an overview tracker that shows individual student performance for all summative assessments in our Algebra II course. The summative assessment overview tracker provides me with a broader outlook on our class progress towards learning goals. My goal is for my classes to have 80% mastery, so this tracker allows me to monitor class mastery for the school year-to-date.

A snapshot of the summative assessment overview tracker is on the right. This mastery tracker can be filtered by class period, student, and objective. I also spot check mastery by grade level, gender, and ability, to reflect on the inclusiveness of my teaching methods. The image above shows that I need to spiral in explicit and recursive arithmetic formulas and graphing quadratics. I noted that these objectives should be spiraled into future homework problems. Overall, the unit on arithmetic and geometric sequences and series was mastered at 81%, so I moved on to teaching the next unit.

Back to Assessments

To the Top

Continue to Year-long Assessments